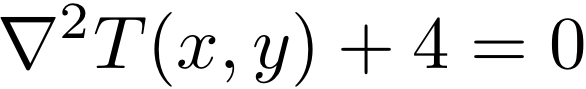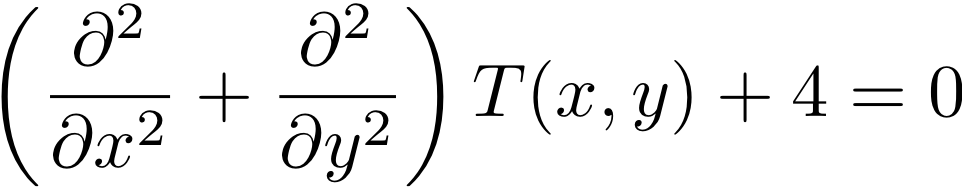- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 6.3 2次元可視化 へ行く。
- 1 (2010-07-08 (木) 12:11:47)
- 2 (2010-07-08 (木) 12:37:23)
- 3 (2010-07-13 (火) 18:51:41)
- 4 (2010-07-14 (水) 15:28:22)
- 5 (2010-07-14 (水) 18:18:29)
- 6 (2010-07-15 (木) 00:11:34)
- 7 (2010-07-15 (木) 10:09:12)
- 8 (2010-07-15 (木) 13:39:47)
- 9 (2010-07-15 (木) 15:46:56)
- 10 (2010-07-15 (木) 19:42:38)
- 11 (2010-07-20 (火) 18:08:30)
- 12 (2010-07-21 (水) 09:46:03)
- 13 (2010-07-23 (金) 14:05:54)
- 14 (2010-08-07 (土) 20:36:59)
- 15 (2011-07-07 (木) 08:45:21)
- 16 (2011-07-13 (水) 20:51:29)
- 17 (2011-07-14 (木) 11:47:06)
- 18 (2011-07-14 (木) 14:01:16)
- 19 (2011-07-16 (土) 22:36:41)
- 20 (2011-07-19 (火) 13:26:18)
- 21 (2011-07-19 (火) 20:49:57)
- 22 (2011-07-20 (水) 16:00:42)
- 23 (2011-07-20 (水) 16:41:26)
- 24 (2011-07-28 (木) 06:37:28)
- 25 (2011-11-15 (火) 16:58:35)
- 26 (2011-12-21 (水) 21:00:53)
- 27 (2011-12-27 (火) 18:25:20)
- 28 (2012-01-24 (火) 15:23:16)
- 29 (2012-05-08 (火) 14:22:10)
- 30 (2012-06-28 (木) 09:53:37)
- 31 (2012-08-28 (火) 16:04:39)
- 32 (2013-01-16 (水) 18:10:58)
- 33 (2013-03-05 (火) 10:45:54)
- 34 (2014-02-19 (水) 09:12:18)
現在(2015-11-07 (土) 15:06:03)作成中です。 既に書いている内容も大幅に変わる可能性が高いので注意。
神戸大学 大学院システム情報学研究科 計算科学専攻 陰山 聡
【目次】
問題設定の復習 †
- 2次元正方形領域 [0,1]×[0,1] での熱伝導を考える
- 境界をすべて0℃に固定
- 領域全体に一定の熱を加える
- ⇒ このとき,十分な時間が経った後での温度分布はどうなるか?
前回の補足 †
- スクリプトでgnuplotを使う場合、グラフがグラフが一瞬描かれた直後に終了してしまうという問題があった。これを避けるにはgnuplotスクリプトの最後の一行に
pause -1
と書く必要があった。
- wiki中、ソースコード部分が等角フォントで表示されていない場合、 別のブラウザを試してみること。 (ソースコード中のコメントは一部、等角フォントを仮定している。)
前回の宿題 †
前回の宿題は、「thermal_diffusion.f90を理解しておくこと」であった。 ここではポイントだけ説明する。
- コード全体の構造
- モジュール構成は以下のとおり:
| モジュール名 | 内容 |
| constants | 定数 |
| parallel | 並列化 |
| temperature | 温度場 |
- main programの構造
データ出力ルーチンを除くとコードの構造は以下のとおり:
call parallel__initialize
call temperature__initialize
do loop = 1 , LOOP_MAX
call temperature__update
end do
call temperature__finalize
call parallel__finalize
ルーチン名を見れば意味は明白であろう。
- thermal_diffusion.f90コードでは、例えばmainプログラム
call parallel__initialize call temperature__initialize call temperature__output_1d_profile call temperature__output_2d_profile
に見られるように、関数名(サブルーチン名)は、「モジュール名」+「アンダースコア二つ」+「その関数の中身を示す言葉」で統一されている。 その関数がどのモジュールで定義されているかがすぐに分かるようにするために工夫である。
- 加熱項の表式
今考えている正方形領域は 一様かつ一定に加熱されている。 その加熱率 heat_source を(ある規格化の下で)4とすると、 定常状態における温度T(x,y)は以下のポアッソン方程式を満たす。
つまり
である。
連続場としての温度場を x、y方向に一様な格子間隔(2次元カーテシアン格子)で離散化し、 2次精度の中心差分法で上のラプラシアンを近似すると、
(T(i+1,j)-2*T(i,j)+T(i-1,j))/dx^2 + (T(i,j+1)-2*T(i,j)+T(i,j-1))/dy^2 + heat_source = 0.
となる。ここでdxとdyはそれぞれx方向とy方向の格子間隔である。 特にdx=dyならば、その値をhと書いて、変形すると
T(i,j) = (T(i+1,j)+T(i-1,j)+T(i,j+1)+T(i,j-1))/4+heat_source*h^2/4.
が得られる。 ヤコビ法ではこの式が成り立つまで温度場Tを繰り返し計算する。
- heat_sourceが一定かつ一様で4という値であれば、右辺第二項は
4*h^2/4
となる。この項は一定なので、ヤコビ法の繰り返し計算で毎回計算するのは馬鹿らしい。 そこで、thermal_diffusion.f90コードでは、subroutine temperature__initialize において
subroutine temperature__initialize real(DP) :: heat_source = 4.0 . . . heat = (heat_source/4) * h * h
としてあらかじめ(一度だけ)計算しておき、その値をheatという変数に保存した上で、 ヤコビ法の繰り返し部分(subroutine temperature__update)では、
subroutine temperature__update
integer :: i, j
.
.
.
do j = jstart, jend
do i = 1, MESH_SIZE
! work(i,j) = (temp(i-1,j)+temp(i+1,j)+temp(i,j-1)+temp(i,j+1))/4.0_DP & ! + heat_source*h*h ! Operation time is saved in below.
work(i,j) = (temp(i-1,j)+temp(i+1,j)+temp(i,j-1)+temp(i,j+1))*0.25_DP &
+ heat
end do
end do
のようにheatという定数を足すだけで済むようにしている。
- 上のコードをよく見ると、コメントアウトされた部分では4.0で割っているところを、 コメントアウトされていない行では0.25を掛けている。 これは割り算よりも掛け算の方が計算が速いからである。
【演習】 テストデータの作成 †
thermal_diffusion.f90をコンパイルし、計算機「scalar」で実行せよ。
2次元可視化 †
今回は2次元データの可視化を行う。 前回と同様gnuplotを利用する。
gnuplotで2次元データをプロットする場合、そのデータのフォーマットは
x00 y00 関数値 x01 y00 関数値 x02 y00 関数値 ・ ・ ・ x09 y00 関数値 (空行) x00 y01 関数値 x01 y01 関数値 x02 y01 関数値 ・ ・ ・ x09 y01 関数値 (空行) ・ ・ ・ x09 y09 関数値
である。
2次元データ出力ルーチン †
thermal_diffusion.f90による2次元データ出力ルーチン temperature__output_2d_profile は、正方形上(x,y平面上)に分布する温度をすべて書き出すものである。 中身を見てみよう。
subroutine temperature__output_2d_profile
real(DP), dimension(0:MESH_SIZE+1, &
0:MESH_SIZE+1) :: prof
integer :: counter = 0 ! saved
integer :: ierr ! use for MPI
integer :: jstart_, jend_
character(len=4) :: serial_num ! put on file name
character(len=*), parameter :: base = "../data/temp.2d."
integer :: i, j
call set_jstart_and_jend(jstart_,jend_)
write(serial_num,'(i4.4)') counter
prof(:,:) = parallel__set_prof_2d(jstart_,jend_,temp(:,jstart_:jend_))
if ( myrank==0 ) then
open(10,file=base//serial_num)
do j = 0 , MESH_SIZE+1
do i = 0 , MESH_SIZE+1
write(10,*) i, j, prof(i,j)
end do
write(10,*)' ' ! gnuplot requires a blank line here.
end do
close(10)
end if
counter = counter + 1
end subroutine temperature__output_2d_profile
【演習】 †
- thermal_diffusion.f90をmpif90コマンドでコンパイルし、
- ジョブスクリプトthermal_diffusion.jsで並列計算せよ。
- 連番つきファイルtemp.2d.????が出力されるはずである。 その中身は以下のようになっているはず。確認せよ。
55 35 0.1165598588705999
56 35 9.9624877672293416E-002
57 35 8.1734108631726782E-002
58 35 6.2857224006520482E-002
59 35 4.2963409431420671E-002
60 35 2.2021479795155254E-002
61 35 0.000000000000000
0 36 0.000000000000000
1 36 2.1867122785152873E-002
2 36 4.2655284590767971E-002
3 36 6.2396502500601705E-002
4 36 8.1122529495226178E-002
・
・
・
57 36 8.1122529495226178E-002
58 36 6.2396502500601705E-002
59 36 4.2655284590767971E-002
60 36 2.1867122785152873E-002
61 36 0.000000000000000
0 37 0.000000000000000
1 37 2.1680615643577435E-002
2 37 4.2282992534786040E-002
3 37 6.1839860798781864E-002
4 37 8.0383668447763873E-002
5 37 9.7946446090882752E-002
6 37 0.1145596782417825
・
・
・
gnuplotによる2次元等高線の表示 †
静止画による説明
【演習】アニメーション †
gnuplotによる2次元カラー表示 †
静止画による説明
【演習】アニメーション †
gnuplotによるsurface表示 †
静止画による説明
【演習】アニメーション †
熱源分布が一様でない場合の平衡温度分布 †
ソースコードの変更。 thermal_diffusion2.f90
レポート課題 01 †
thermal_diffusion02.f90で求めたチェッカーボード型熱源分布の平衡解(最終状態解)を可視化せよ。 温度の最大値と最小値も記せ。
授業アンケート †
今回の演習内容はどうでしたか?(どれか一つ、一度だけ押してください。)
2次元領域分割による並列化 †
質問、コメントなど自由にどうぞ †
「お名前」欄は空欄で可。
最新の10件を表示しています。 コメントページを参照
as of 2025-07-03 (木) 23:14:29 (6223)