- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 7.実践編 へ行く。
- 1 (2010-07-14 (水) 17:40:14)
- 2 (2010-07-14 (水) 20:19:44)
- 3 (2010-07-15 (木) 00:07:29)
- 4 (2010-07-15 (木) 13:41:50)
- 5 (2010-07-21 (水) 12:27:05)
- 6 (2010-07-21 (水) 23:23:55)
- 7 (2010-07-22 (木) 00:52:46)
- 8 (2010-07-22 (木) 10:15:00)
- 9 (2010-07-22 (木) 12:34:39)
- 10 (2010-07-22 (木) 13:53:00)
- 11 (2010-07-22 (木) 20:51:23)
- 12 (2010-07-23 (金) 09:25:49)
- 13 (2010-07-23 (金) 16:05:34)
- 14 (2010-07-27 (火) 15:11:07)
- 15 (2010-07-29 (木) 15:29:22)
- 16 (2010-08-16 (月) 11:59:53)
- 17 (2011-07-13 (水) 20:38:34)
- 18 (2011-07-20 (水) 20:49:05)
- 19 (2011-07-21 (木) 11:32:31)
- 20 (2011-07-21 (木) 15:17:08)
- 21 (2011-07-26 (火) 14:31:02)
- 22 (2011-07-27 (水) 19:24:22)
- 23 (2011-07-28 (木) 18:10:42)
- 24 (2011-07-30 (土) 16:29:58)
- 25 (2011-07-31 (日) 17:41:32)
- 26 (2012-06-20 (水) 16:43:09)
- 27 (2012-11-01 (木) 21:18:14)
- 28 (2013-02-17 (日) 10:03:31)
- 29 (2013-05-14 (火) 00:36:08)
- 30 (2013-06-19 (水) 20:46:21)
- 31 (2013-07-18 (木) 09:43:32)
- 32 (2014-07-17 (木) 11:00:59)
- 33 (2014-07-18 (金) 09:03:36)
- 34 (2014-07-18 (金) 09:03:48)
- 35 (2015-07-16 (木) 11:32:39)
- 36 (2016-07-21 (木) 10:36:50)
- 37 (2016-07-28 (木) 11:32:05)
- 38 (2017-07-19 (水) 20:09:16)
- 39 (2017-07-19 (水) 20:09:46)
- 40 (2017-07-20 (木) 14:49:27)
- 41 (2017-07-24 (月) 16:23:38)
- 42 (2017-07-27 (木) 14:50:35)
- 43 (2017-07-27 (木) 18:30:54)
神戸大学 大学院システム情報学研究科 計算科学専攻 陰山 聡
- 今回の演習で使うコードは
/tmp/100722
にある。
- 前回のレポート課題に出した市松模様の加熱を行うコードは
/tmp/100722/thermal_diffusion_checker.f90
に置いた。
【目次】
- 2次元並列化
- そもそも1次元(低次元)並列化が不可能な場合
- 通信量時間の問題
- 計算と通信
- 1次元領域分割と2次元領域分割
- 2次元領域分割の方法
- 性能測定法
- cpu_time関数の利用例
- stopwatchモジュールの利用法
- 2次元領域分割による並列コード
- 【演習】2次元領域分割による並列化コードの実行(非並列計算)
- 【演習】2次元領域分割による並列化コードの実行(並列計算1)
- 【演習】2次元領域分割による並列化コードの実行(並列計算2)
- 1次元領域分割と2次元領域分割の差
- デュアルコアの利用
- 【演習】flat MPI並列化
- hybrid並列化
- hybrid並列化法による熱伝導コード
- 【演習】hybrid並列化
- レポート課題
- レポート提出方法
- アンケート
2次元並列化 †
- 引き続き、正方形領域の熱伝導問題(平衡温度分布)を解く例題を扱う。
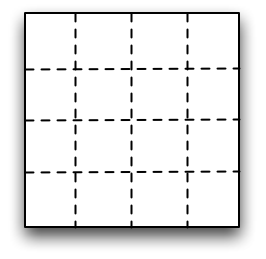
- これまでMPIで並列化を行うにあたり、正方形領域のy方向(j方向)に複数の領域に分割し、 それぞれの領域に一つずつMPIプロセスを割り当てて並列化していた。 このような並列化を1次元領域分割による並列化という。 下の図は正方形領域を16個の領域に分割した例である。
- 同様に二次元領域分割による並列化も考えられる。 正方形を16個の領域に2次元的に分割すると下の図のようになる。
- 上の二つの図の場合、どちらも16個のMPIプロセスで並列化している。 計算を早く終了させるためには、どちらが有利だろうか? 今回はまずこのような、領域分割に基づく並列化を行う場合の、分割の次元数について考える。
そもそも1次元(低次元)並列化が不可能な場合 †
- 今考えている熱伝導問題の格子サイズMESH_SIZEが60、並列計算に利用出来るプロセッサコアの総数が100個あったとしよう。 (今回の演習で利用している計算機 "scalar" は最大128コアを利用出来るジョブが投入できる。) この時、前回使った1次元領域分割に基づく並列化(thermal_diffusion.f90)はできない。 y方向(j方向に)60個ある格子点を100個に分割することができないからである。
- 2次元領域分割なら可能である。x方向(i方向)に10、y方向(j方向)に10、合計100個の領域に分割すれば、100個のコアを利用した並列計算が可能である。
- 解くべき問題が3次元であれば(例えば立方体中の熱伝導問題など)、1次元で領域分割が不可能である場合も、2次元や3次元で領域分割が可能な場合がある。
通信量時間の問題 †
- たとえば、MESH_SIZE が1000であれば、100個のコアを使った1次元領域分割は十分可能である。 この場合、1次元領域分割と2次元領域分割は計算速度(答えを得るまでの時間)の点で同じであろうか? 一つあたりのプロセッサが担当する(計算する)領域は全体正方形の1/100の面積に相当するので、どちらのやりかたで分割しても同じかと思うかもしれない。
- だがそれは違う。 プロセス間の通信にかかる時間がゼロであればそのとおりだが、実際にはプロセス間の通信(MPI_SENDやMPI_RECV等)には有限の―それどころか結構長い―時間がかかる。
- では、プロセス間通信に長い時間がかかるという前提の下で、 1次元領域分割と、2次元領域分割ではどちらが有利であろうか?
計算と通信 †
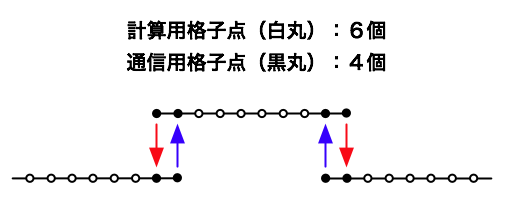
- 1次元空間を格子点で離散化した上で、MPIでプロセス間通信を行う場合を考える。
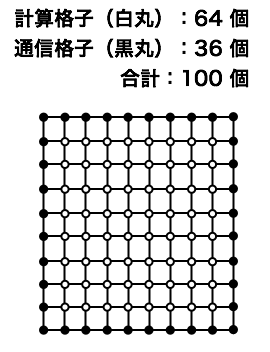
- 計算格子には2種類ある。一つは、その上で計算だけを行う格子。 もう一つはMPI通信のデータを送ったり、受けたりする格子である。 (一番外側から2番目の格子は計算も通信も行う。)
- 一つのMPIプロセスが行う通信の量は、通信を行う格子点の数に比例する。 通信に時間がかかる場合、通信を行う格子点は少ないほうが望ましい。
1次元領域分割と2次元領域分割 †
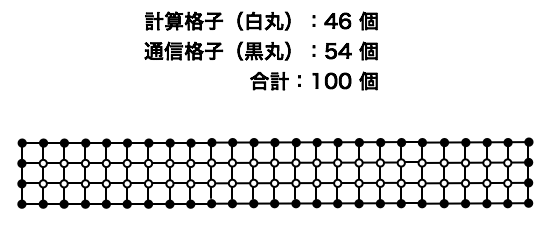
- 下の図は正方形領域を400個の格子点で離散化した場合を示す。
- これを4つのMPIプロセスで並列化することを考える。 1次元領域分割の場合、下の図のようになる。
- 2次元領域分割の場合、同じく4つのMPIプロセスで並列化すると、下の図のようになる。
- 1次元領域分割の場合、一番下(赤色)のMPIプロセスが担当する長方形の領域の中で、通信をおこなう格子点は長方形の辺上にあるものである。数えてみるとその数は46個。
- 2次元領域分割の場合、左下のMPIプロセス(赤色)が担当するのは正方形領域である。 この中で通信をおこなう格子点はこの正方形の辺上にあるもので、数えてみると38個。
- 1次元領域分割は2次元領域分割に比べて一つのプロセッサあたり46-38=8個の格子点数分だけ通信するデータ量が多い。 プロセス間の通信速度が低い場合、できるだけ通信するデータの量を減らす必要がある。 この点で、2次元領域分割の方が有利である。
- ただし、実際には、コアとメモリ間との通信速度(キャッシュの利用効率)の影響等により、必ずしも2次元領域分割の方が速いというわけではない。
- キャッシュの利用効率を上げる方法は研究の現場では重要なテーマであるが、この演習では取り上げない。
2次元領域分割の方法 †
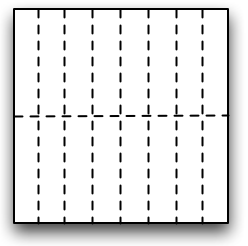
- 同じMPIプロセス数による2次元領域分割でも様々な可能性がある。 たとえば、正方形を16個の長方形に分割する場合、次の二つではどちらが通信量が少ないであろうか?
- 正方形を16個に分割するのだから、どちらも方法でも一つのMPIプロセスが担当する面積は等しい(元の正方形の16分の1)。 だが、下の二つの図を見ればわかるとおり、長方形よりも正方形に近い方が通信量が少ない。
- 面積の等しい長方形の中で、4辺の長さの合計が最も小さいものは正方形である、という幾何学的事実を思い出せばこれは自明であろう。
性能測定法 †
- 1次元領域分割による並列コードと2次元領域分割に基づく並列コードの速度を比較する前に、 計算に要する時間やMPI通信に要する時間を測定する方法について説明する。
- これまで以下の二つの方法を説明した。
- 「4. OpenMP入門」では、omp_get_wtime()関数による時間測定
- 「5. MPIを用いた並列計算」では、mpi_wtime()関数による時間測定
- 今回はもう一つの方法を紹介する:
- Fotran95言語の組み込み関数(サブルーチン) cpu_time()による時間測定
- 仕様
subroutine cpu_time(time) real(SP), intent(out) :: time !プログラムの始まりから計測したCPU時間(秒)
- mpi_wtimeは、MPIを用いた並列化プログラムのみで、しかもmpi_initを呼んだ後でしか使えなかったが、cpu_timeにはそのような制限がない。(ただしFotran95で導入された関数なので、古いFotran90コンパイラは対応していないかもしれない。)
cpu_time関数の利用例 †
- stopwatchモジュール
module stopwatch
use constants
implicit none
private
public :: stopwatch__print, stopwatch__strt, stopwatch__stop
integer, parameter :: max_watch_id = 100
integer :: used_watch_id_max=-1
real(SP), dimension(0:max_watch_id) :: time_start_saved, time_total
contains
subroutine stopwatch__print
integer :: id
do id = 0 , used_watch_id_max
print *,'stopwatch:', id, time_total(id)
end do
end subroutine stopwatch__print
subroutine stopwatch__strt(id)
integer, intent(in) :: id
logical :: firstcall = .true.
if (firstcall) then
time_total(:) = 0.0_DP
firstcall = .false.
end if
if (id>used_watch_id_max) used_watch_id_max = id
call cpu_time(time_start_saved(id))
end subroutine stopwatch__strt
subroutine stopwatch__stop(id)
integer, intent(in) :: id
real(SP) :: time_now, elapsed
call cpu_time(time_now)
elapsed = time_now - time_start_saved(id)
time_total(id) = time_total(id) + elapsed
end subroutine stopwatch__stop
end module stopwatch
stopwatchモジュールの利用法 †
program thermal_diffusion_decomp2d_hybrid
use constants
use parallel
use temperature
use stopwatch
implicit none
integer :: loop
call stopwatch__strt(0) ! プログラム全体の実行時間
call stopwatch__strt(1) ! 並列化初期化にかかる時間
call parallel__initialize
call stopwatch__stop(1)
call stopwatch__strt(2) ! 温度場初期化にかかる時間
call temperature__initialize
call stopwatch__stop(2) ! 温度場の出力にかかる時間
call temperature__output_2d_profile
call stopwatch__stop(2)
call stopwatch__strt(3) ! ヤコビ法による求解にかかる時間
do loop = 1 , LOOP_MAX
call temperature__update
end do
call stopwatch__stop(3)
call stopwatch__stop(0)
call stopwatch__print ! 結果の出力
call temperature__finalize
call parallel__finalize
end program thermal_diffusion_decomp2d_hybrid
- 出力例
stopwatch: 0 1.286565 stopwatch: 1 0.2393930 stopwatch: 2 4.3821335E-04 stopwatch: 3 1.046950
- これを見るとプログラム全体の実行時間(0番)のうち、ほとんどがヤコビ法の求解(3番)に費やされていることがわかる。
2次元領域分割による並列コード †
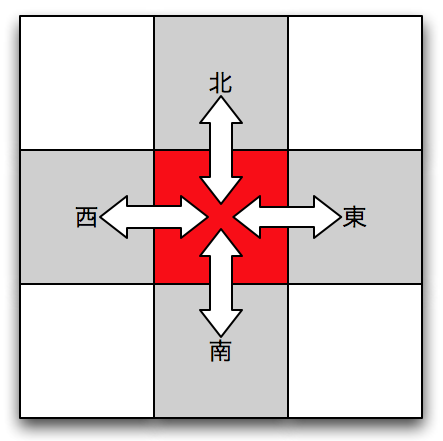
- 領域分割による並列化を行うときに注意すべき点は、 MPIプロセスの配置方法である。 2次元領域分割の場合、あるプロセスに注目すると、最も頻繁に通信する相手は、隣(東西南北)の4つのプロセスである。
- 計算機のネットワークの配線方法(トポロジー)等に基づく通信性能の特性を考慮に入れて、 隣同士の通信がもっとも通信速度的に「近い」位置にプロセスを配置することが望ましい。
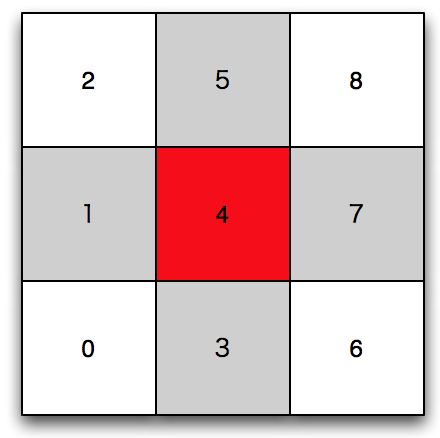
- 以下のようにプロセス(ランク番号)を配置した場合、 4番のプロセスはランク番号1,3,5,7のプロセスと頻繁に通信することになる。
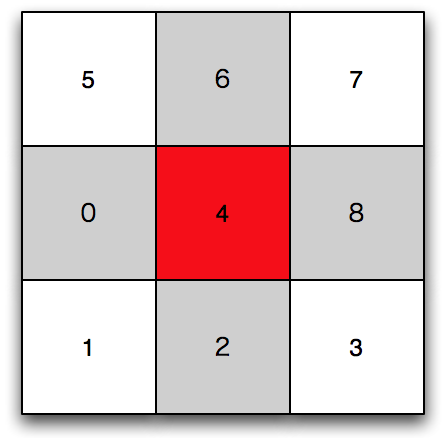
- もしも使用している並列計算機のネットワークの設計上、 4番のプロセスはむしろランク番号0,2,6,8のプロセスと通信した方が速い場合には、以下のようにプロセスを配置する方が望ましい。
- MPI関数の一つMPI_CART_CREATEを使うと、もしも使用する計算機がネットワークの通信性能の関する情報を提供している場合には、その情報を活用し通信効率の点で最適な配置でプロセスを自動的に分配してくれる。
- MPI_CART_CREATEを用いた2次元領域分割法による熱伝導問題のコード thermal_diffusion_decomp2d.f90 を示す。 MPI_SENDRECV関数を用いて東西南北の4つの隣接プロセスと通信する。
!=========================================================================
! thermal_diffusion_decomp2d_mpi.f90
!
! Purpose:
! To calcuate thermal equilibrium state, or the temperature
! distribution T(x,y) in a unit square, 0<=(x,y)<=1.
! Heat source is constant and uniform in the square.
! Temperature's boundary condition is fixed; T=0 on the four
! sides.
!
! Method:
! 2nd order finite difference approximation for the Poisson
! equation of the temperature,
! \nabla^2 T(x,y) + heat_source = 0.
! leads to
! T(i,j) = (T(i+1,j)+T(i-1,j)+T(i,j+1)+T(i,j-1)) / 4 &
! + heat_source*h^2/4,
! where the grid spacing, h, is same and uniform in x-
! and y-directions. Jacobi method is used to solve this.
!
! Parallelization:
! MPI parallelization under 2-dimensional domain decomposition.
!
! Reference codes:
! - "thermal_diffusion.f90" is a companion code that is
! parallelized with a 1-D domain decomposition.
! - "sample_birdseyeview.gp" is a gnuplot script to visualize
! T(i,j) distribution in the square, produced by the routine
! temperature__output_2d_profile in this code.
!
! Coded by Akira Kageyama,
! at Kobe University,
! on 2010.07.15,
! for the Lecture Series "Computational Science" (2010).
!=========================================================================
module constants
implicit none
integer, parameter :: SP = kind(1.0)
integer, parameter :: DP = selected_real_kind(2*precision(1.0_SP))
integer, parameter :: MESH_SIZE = 1000 ! was = 61
integer, parameter :: LOOP_MAX = 10000
end module constants
module stopwatch
use constants
implicit none
private
public :: stopwatch__print, stopwatch__strt, stopwatch__stop
integer, parameter :: max_watch_id = 100
integer :: used_watch_id_max=-1
real(SP), dimension(0:max_watch_id) :: time_start_saved, time_total
contains
subroutine stopwatch__print
integer :: id
do id = 0 , used_watch_id_max
print *,'stopwatch:', id, time_total(id)
end do
end subroutine stopwatch__print
subroutine stopwatch__strt(id)
integer, intent(in) :: id
logical :: firstcall = .true.
if (firstcall) then
time_total(:) = 0.0_DP
firstcall = .false.
end if
if (id>used_watch_id_max) used_watch_id_max = id
call cpu_time(time_start_saved(id))
end subroutine stopwatch__strt
subroutine stopwatch__stop(id)
integer, intent(in) :: id
real(SP) :: time_now, elapsed
call cpu_time(time_now)
elapsed = time_now - time_start_saved(id)
time_total(id) = time_total(id) + elapsed
end subroutine stopwatch__stop
end module stopwatch
module parallel
use constants
use mpi
implicit none
private
public :: parallel__initialize, &
parallel__i_am_on_border, &
parallel__communicate, &
parallel__finalize, &
parallel__set_prof_2d, &
parallel__tellme
type ranks_
integer :: me
integer :: north, south, west, east
end type ranks_
type(ranks_) :: ranks
integer, parameter :: ndim = 2 ! 2-D domain decomposition
type process_topology_
integer :: comm
integer, dimension(ndim) :: dims
integer, dimension(ndim) :: coords
end type process_topology_
type(process_topology_) :: cart2d
integer :: nprocs
integer :: istt, iend
integer :: jstt, jend
contains
!== Private ==!
subroutine dataTransferEastward(n,sent_vect, recv_vect)
integer, intent(in) :: n
real(DP), dimension(n), intent(in) :: sent_vect
real(DP), dimension(n), intent(out) :: recv_vect
integer :: ierr
integer, dimension(MPI_STATUS_SIZE) :: status
call mpi_sendrecv(sent_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%east, &
0, &
recv_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%west, &
MPI_ANY_TAG, &
cart2d%comm, &
status, &
ierr)
end subroutine dataTransferEastward
subroutine dataTransferNorthward(n,sent_vect, recv_vect)
integer, intent(in) :: n
real(DP), dimension(n), intent(in) :: sent_vect
real(DP), dimension(n), intent(out) :: recv_vect
integer :: ierr
integer, dimension(MPI_STATUS_SIZE) :: status
call mpi_sendrecv(sent_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%north, &
0, &
recv_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%south, &
MPI_ANY_TAG, &
cart2d%comm, &
status, &
ierr)
end subroutine dataTransferNorthward
subroutine dataTransferSouthward(n,sent_vect, recv_vect)
integer, intent(in) :: n
real(DP), dimension(n), intent(in) :: sent_vect
real(DP), dimension(n), intent(out) :: recv_vect
integer :: ierr
integer, dimension(MPI_STATUS_SIZE) :: status
call mpi_sendrecv(sent_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%south, &
0, &
recv_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%north, &
MPI_ANY_TAG, &
cart2d%comm, &
status, &
ierr)
end subroutine dataTransferSouthward
subroutine dataTransferWestward(n,sent_vect, recv_vect)
integer, intent(in) :: n
real(DP), dimension(n), intent(in) :: sent_vect
real(DP), dimension(n), intent(out) :: recv_vect
integer :: ierr
integer, dimension(MPI_STATUS_SIZE) :: status
call mpi_sendrecv(sent_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%west, &
0, &
recv_vect, &
n, &
MPI_DOUBLE_PRECISION, &
ranks%east, &
MPI_ANY_TAG, &
cart2d%comm, &
status, &
ierr)
end subroutine dataTransferWestward
!== Public ==!
subroutine parallel__communicate(ism1,iep1,jsm1,jep1,field)
integer, intent(in) :: ism1, iep1, jsm1, jep1
real(DP), dimension(ism1:iep1,jsm1:jep1), intent(inout) :: field
integer :: ierr
integer, dimension(MPI_STATUS_SIZE) :: status
integer :: i, j, istt, iend, jstt, jend, isize, jsize
real(DP), dimension(MESH_SIZE+2) :: sent_vect, recv_vect
! real(DP), dimension(:), allocatable :: sent_vect, recv_vect
istt = ism1 + 1
iend = iep1 - 1
jstt = jsm1 + 1
jend = jep1 - 1
isize = iep1 - ism1 + 1
! allocate(sent_vect(isize),recv_vect(isize))
sent_vect(1:isize) = field(ism1:iep1,jend)
call dataTransferNorthward(isize,sent_vect,recv_vect)
field(ism1:iep1,jsm1) = recv_vect(1:isize)
sent_vect(1:isize) = field(ism1:iep1,jstt)
call dataTransferSouthward(isize,sent_vect,recv_vect)
field(ism1:iep1,jep1) = recv_vect(1:isize)
! deallocate(sent_vect,recv_vect)
jsize = jend - jstt + 1
! allocate(sent_vect(jsize),recv_vect(jsize))
sent_vect(1:jsize) = field(iend,jstt:jend)
call dataTransferEastward(jsize,sent_vect,recv_vect)
field(ism1,jstt:jend) = recv_vect(1:jsize)
sent_vect(1:jsize) = field(istt,jstt:jend)
call dataTransferWestward(jsize,sent_vect,recv_vect)
field(iep1,jstt:jend) = recv_vect(1:jsize)
! deallocate(sent_vect,recv_vect)
end subroutine parallel__communicate
subroutine parallel__finalize
integer :: ierr
call mpi_finalize(ierr)
end subroutine parallel__finalize
function parallel__i_am_on_border(which) result(answer)
character(len=*), intent(in) :: which
logical :: answer
answer = .false.
if ( which=='west' .and.cart2d%coords(1)==0 ) answer = .true.
if ( which=='east' .and.cart2d%coords(1)==cart2d%dims(1)-1 ) answer = .true.
if ( which=='south'.and.cart2d%coords(2)==0 ) answer = .true.
if ( which=='north'.and.cart2d%coords(2)==cart2d%dims(2)-1 ) answer = .true.
end function parallel__i_am_on_border
subroutine parallel__initialize
logical, dimension(ndim) :: is_periodic
integer :: ierr
logical :: reorder
call mpi_init(ierr)
call mpi_comm_size(MPI_COMM_WORLD, nprocs, ierr)
cart2d%dims(:) = 0 ! required by mpi_dims_create
call mpi_dims_create(nprocs, ndim, cart2d%dims, ierr)
is_periodic(1) = .false.
is_periodic(2) = .false.
reorder = .true.
call mpi_cart_create(MPI_COMM_WORLD, ndim, cart2d%dims, &
is_periodic, reorder, cart2d%comm, ierr)
call mpi_comm_rank (cart2d%comm, ranks%me, ierr)
call mpi_cart_shift(cart2d%comm, 0, 1, &
ranks%west, ranks%east, ierr)
call mpi_cart_shift(cart2d%comm, 1, 1, &
ranks%south, ranks%north, ierr)
call mpi_cart_coords(cart2d%comm, ranks%me, 2, cart2d%coords, ierr)
print *,' dims(1) = ', cart2d%dims(1)
print *,' dims(2) = ', cart2d%dims(2)
print *,' coords(1) = ', cart2d%coords(1)
print *,' coords(2) = ', cart2d%coords(2)
istt = MESH_SIZE * cart2d%coords(1) / cart2d%dims(1) + 1
iend = MESH_SIZE * (cart2d%coords(1)+1) / cart2d%dims(1)
jstt = MESH_SIZE * cart2d%coords(2) / cart2d%dims(2) + 1
jend = MESH_SIZE * (cart2d%coords(2)+1) / cart2d%dims(2)
print *,' nprocs = ', nprocs
print *,' ranks%me = ', ranks%me
print *,' istt = ', istt, ' iend = ', iend
print *,' jstt = ', jstt, ' jend = ', jend
print *,' north = ', ranks%north
print *,' south = ', ranks%south
print *,' west = ', ranks%west
print *,' east = ', ranks%east
print *,' i_am_on_border("west") = ', parallel__i_am_on_border("west")
print *,' i_am_on_border("east") = ', parallel__i_am_on_border("east")
print *,' i_am_on_border("north") = ', parallel__i_am_on_border("north")
print *,' i_am_on_border("south") = ', parallel__i_am_on_border("south")
end subroutine parallel__initialize
function parallel__set_prof_2d(ism1,iep1, &
jsm1,jep1, &
istt_,iend_, &
jstt_,jend_, &
myprof) result(prof_2d)
integer, intent(in) :: ism1
integer, intent(in) :: iep1
integer, intent(in) :: jsm1
integer, intent(in) :: jep1
integer, intent(in) :: istt_
integer, intent(in) :: iend_
integer, intent(in) :: jstt_
integer, intent(in) :: jend_
real(DP), dimension(ism1:iep1,jsm1:jep1), intent(in) :: myprof
real(DP), dimension(0:MESH_SIZE+1,0:MESH_SIZE+1) :: prof_2d
real(DP), dimension(0:MESH_SIZE+1,0:MESH_SIZE+1) :: work
integer :: ierr
integer :: meshsize_p1_sq = (MESH_SIZE+1)**2
work(:,:) = 0.0_DP
work(istt_:iend_,jstt_:jend_) = myprof(istt_:iend_,jstt_:jend_)
call mpi_allreduce(work(1,1), & ! source
prof_2d(1,1), & ! target
meshsize_p1_sq, &
MPI_DOUBLE_PRECISION, &
MPI_SUM, &
cart2d%comm, &
ierr)
end function parallel__set_prof_2d
function parallel__tellme(which) result(val)
character(len=*), intent(in) :: which
integer :: val
select case (which)
case ('rank_east')
val = ranks%east
case ('rank_north')
val = ranks%north
case ('rank_south')
val = ranks%south
case ('rank_west')
val = ranks%west
case ('rank_me')
val = ranks%me
case ('iend')
val = iend
case ('istt')
val = istt
case ('jend')
val = jend
case ('jstt')
val = jstt
case ('nprocs')
val = nprocs
case default
print *, 'Bad arg in parallel__tellme.'
call parallel__finalize
stop
end select
end function parallel__tellme
end module parallel
module temperature
use constants
use stopwatch
use parallel
implicit none
private
public :: temperature__initialize, &
temperature__finalize, &
temperature__output_2d_profile, &
temperature__update
real(DP), allocatable, dimension(:,:) :: temp
real(DP), allocatable, dimension(:,:) :: work
real(DP), parameter :: SIDE = 1.0_DP
real(DP) :: h = SIDE / (MESH_SIZE+1)
real(DP) :: heat
integer :: istt, iend, jstt, jend
integer :: myrank, north, south, west, east, nprocs
contains
!=== Private ===
subroutine boundary_condition
if ( parallel__i_am_on_border('west') ) temp( 0,jstt-1:jend+1) = 0.0_DP
if ( parallel__i_am_on_border('east') ) temp( MESH_SIZE+1,jstt-1:jend+1) = 0.0_DP
if ( parallel__i_am_on_border('north') ) temp(istt-1:iend+1, MESH_SIZE+1) = 0.0_DP
if ( parallel__i_am_on_border('south') ) temp(istt-1:iend+1, 0) = 0.0_DP
end subroutine boundary_condition
!=== Public ===
subroutine temperature__initialize
real(DP) :: heat_source = 4.0
istt = parallel__tellme('istt')
iend = parallel__tellme('iend')
jstt = parallel__tellme('jstt')
jend = parallel__tellme('jend')
myrank = parallel__tellme('rank_me')
north = parallel__tellme('rank_north')
south = parallel__tellme('rank_south')
east = parallel__tellme('rank_east')
west = parallel__tellme('rank_west')
nprocs = parallel__tellme('nprocs')
allocate(temp(istt-1:iend+1,jstt-1:jend+1))
allocate(work( istt:iend , jstt:jend) )
heat = (heat_source/4) * h * h
temp(:,:) = 0.0_DP ! initial condition
end subroutine temperature__initialize
subroutine temperature__finalize
deallocate(work,temp)
end subroutine temperature__finalize
subroutine temperature__output_2d_profile
real(DP), dimension(0:MESH_SIZE+1, &
0:MESH_SIZE+1) :: prof
integer :: counter = 0 ! saved
integer :: ierr ! use for MPI
integer :: istt_, iend_, jstt_, jend_
character(len=4) :: serial_num ! put on file name
character(len=*), parameter :: base = "../data/temp.2d."
integer :: i, j
call set_istt_and_iend
call set_jstt_and_jend
write(serial_num,'(i4.4)') counter
prof(:,:) = parallel__set_prof_2d(istt-1, iend+1, &
jstt-1, jend+1, &
istt_, iend_, &
jstt_, jend_, &
temp)
if ( myrank==0 ) then
open(10,file=base//serial_num)
do j = 0 , MESH_SIZE+1
do i = 0 , MESH_SIZE+1
write(10,*) i, j, prof(i,j)
end do
write(10,*)' ' ! gnuplot requires a blank line here.
end do
close(10)
end if
counter = counter + 1
contains
subroutine set_istt_and_iend
istt_ = istt
iend_ = iend
if ( parallel__i_am_on_border('west') ) then
istt_ = 0
end if
if ( parallel__i_am_on_border('east') ) then
iend_ = MESH_SIZE+1
end if
end subroutine set_istt_and_iend
subroutine set_jstt_and_jend
jstt_ = jstt
jend_ = jend
if ( parallel__i_am_on_border('south') ) then
jstt_ = 0
end if
if ( parallel__i_am_on_border('north') ) then
jend_ = MESH_SIZE+1
end if
end subroutine set_jstt_and_jend
end subroutine temperature__output_2d_profile
subroutine temperature__update
integer :: i, j
call stopwatch__strt(8)
call stopwatch__strt(4)
call parallel__communicate(istt-1,iend+1,jstt-1,jend+1,temp)
call stopwatch__stop(4)
call stopwatch__strt(5)
call boundary_condition
call stopwatch__stop(5)
call stopwatch__strt(6)
do j = jstt , jend
do i = istt , iend
work(i,j) = (temp(i-1,j)+temp(i+1,j)+temp(i,j-1)+temp(i,j+1))*0.25_DP &
+ heat
end do
end do
call stopwatch__stop(6)
call stopwatch__strt(7)
temp(istt:iend,jstt:jend) = work(istt:iend,jstt:jend)
call stopwatch__stop(7)
call stopwatch__stop(8)
end subroutine temperature__update
end module temperature
program thermal_diffusion_decomp2d_mpi
use constants
use parallel
use temperature
use stopwatch
implicit none
integer :: loop
call stopwatch__strt(0)
call stopwatch__strt(1)
call parallel__initialize
call stopwatch__stop(1)
call stopwatch__strt(2)
call temperature__initialize
call stopwatch__stop(2)
!-- call temperature__output_2d_profile
call stopwatch__stop(2)
call stopwatch__strt(3)
do loop = 1 , LOOP_MAX
call temperature__update
!-- if ( mod(loop,100)==0 ) call temperature__output_2d_profile
end do
call stopwatch__stop(3)
call stopwatch__stop(0)
call stopwatch__print
call temperature__finalize
call parallel__finalize
end program thermal_diffusion_decomp2d_mpi
【演習】2次元領域分割による並列化コードの実行(非並列計算) †
- 上のコード thermal_diffusion_decomp2d_mpi.f90を、MESH_SIZE=1000のまま計算機 "scalar" で実行せよ。 使用ノード数は1とする。
- 参考ジョブスクリプト( thermal_diffusion_decomp2d_mpi.js )
#!/bin/sh
#PBS -l cputim_job=00:05:00
#PBS -l memsz_job=2gb
#PBS -l cpunum_job=1
#PBS -T vltmpi
#PBS -b 1
#PBS -q PCL-A
cd /home/users/your_directory/src
mpirun_rsh -np 1 ${NQSII_MPIOPTS} ./a.out
- 実行結果例(抜粋、コメント追加)
[0] stopwatch: 0 156.9908 # 全実行時間 (約157秒) [0] stopwatch: 1 6.5398932E-02 # 並列初期化にかかった時間 [0] stopwatch: 2 1.7432213E-02 # 温度場初期化にかかった時間 [0] stopwatch: 3 156.9167 # temperature__updateにかかった時間 [0] stopwatch: 4 0.8027854 # MPI通信にかかった時間 [0] stopwatch: 5 0.2311089 # 境界条件の設定にかかった時間 [0] stopwatch: 6 90.23702 # ヤコビ法のメインループにかかった時間 [0] stopwatch: 7 65.61881 # 作業配列を温度場にコピーするのにかかった時間 [0] stopwatch: 8 156.9118 # temperature__updateにかかった時間
【演習】2次元領域分割による並列化コードの実行(並列計算1) †
- 今度は同じ計算を、10ノード(10個のプロセッサコア)を使い、10並列で計算してみよう。
- 上のthermal_diffusion_decomp2d_mpi.js のうち、次の2箇所を変える。
- ノード数を10(#PBS -bで指定)にする。
- mpirun_rsh の -np オプションで10とする。
- stopwatchモジュールの出力結果を見ると
[0] stopwatch: 0 15.07710 # 全実行時間 (約15秒) [0] stopwatch: 1 0.3075731 # 並列初期化にかかった時間 [0] stopwatch: 2 1.6336441E-03 # 温度場初期化にかかった時間 [0] stopwatch: 3 14.76871 # temperature__updateにかかった時間 [0] stopwatch: 4 0.6982038 # MPI通信にかかった時間 [0] stopwatch: 5 2.9568195E-02 # 境界条件の設定にかかった時間 [0] stopwatch: 6 8.654255 # ヤコビ法のメインループにかかった時間 [0] stopwatch: 7 5.371924 # 作業配列を温度場にコピーするのにかかった時間 [0] stopwatch: 8 14.76621 # temperature__updateにかかった時間
- 10並列化することで計算速度が1/10になったことがわかる。 MPIの通信に要する時間は全体の計算時間に比べたら無視できるほど小さい。
【演習】2次元領域分割による並列化コードの実行(並列計算2) †
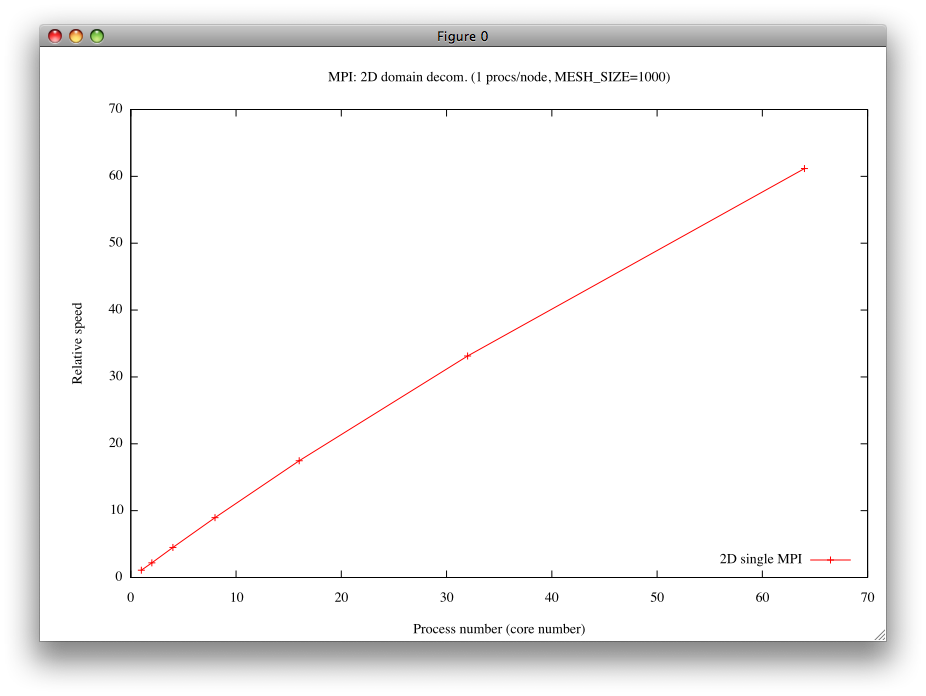
- 今度は同じ計算を、64ノード(64個のプロセッサコア)を使った、64並列で計算してみよう。
[0] stopwatch: 0 3.183086 # 全実行時間 (約3.2秒) [0] stopwatch: 1 0.4711061 # 並列初期化にかかった時間 [0] stopwatch: 2 3.3569336E-04 # 温度場初期化にかかった時間 [0] stopwatch: 3 2.711810 # temperature__updateにかかった時間 [0] stopwatch: 4 0.4736750 # MPI通信にかかった時間 [0] stopwatch: 5 1.4100790E-02 # 境界条件の設定にかかった時間 [0] stopwatch: 6 1.366545 # ヤコビ法のメインループにかかった時間 [0] stopwatch: 7 0.8431044 # 作業配列を温度場にコピーするのにかかった時間 [0] stopwatch: 8 2.709322 # temperature__updateにかかった時間
- gnuplotを使って使用コア数とスピードの関係をグラフにするとこうなる:
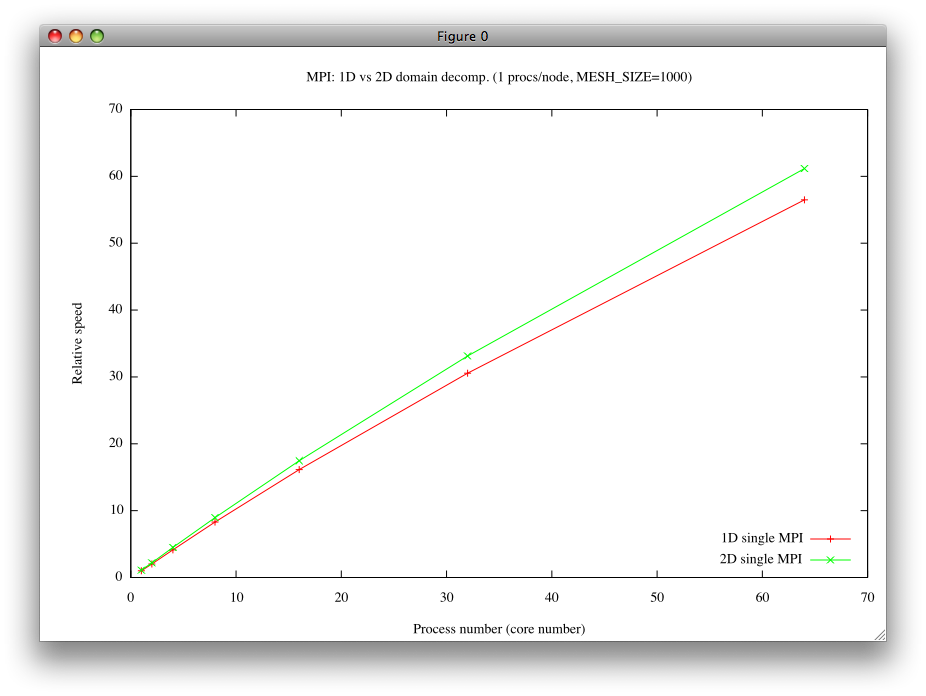
1次元領域分割と2次元領域分割の差 †
- 二つの方法による速度に比較を下のグラフに示す:
- 予想通り2次元領域分割の方が速い。
デュアルコアの利用 †
- これまで使っていたジョブスクリプトを(例えば、今日使った thermal_diffusion_decomp2d_mpi.js)を見ると、常に1ノードに1つのコアを使っていた。
#!/bin/sh ・ ・ #PBS -l cpunum_job=1 ← 1ノードに1つのコアを使う。 ・ ・ ・
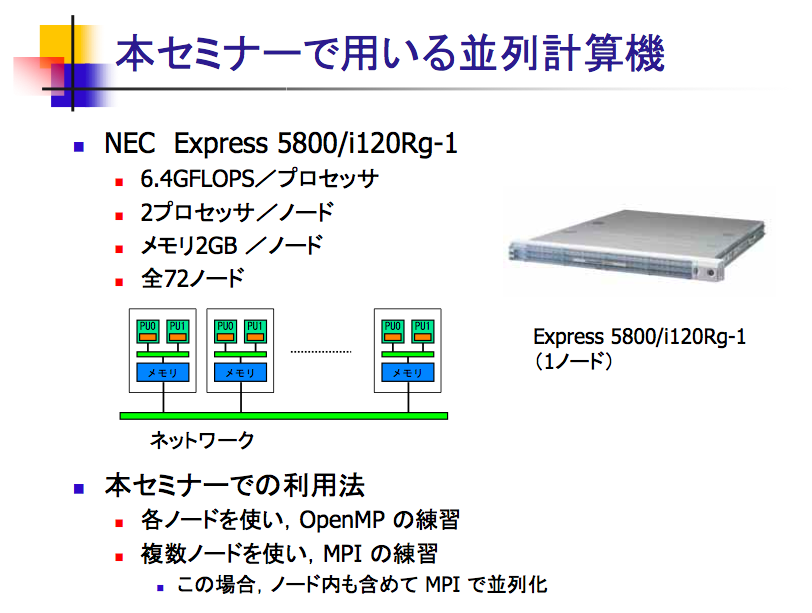
- "scalar"はデュアルコアプロセッサを並列に接続した計算機である。 もういちどscalarの構成を見てみよう。(「3. 並列計算とは」p.17より引用。)
- 上のジョブスクリプトは、ディアルコアのうちひとつしか使っていないことを意味する。 もう一つは遊んでいる。
- 遊ばせておくのはもったいないので、ディアルコアの二つとも使ってみよう。
- ディアルコアプロセッサの二つのコアを使う方法は二つある。 一つはMPIプロセスを二つ走らせる方法。 もう一つはOpenMPでスレッドを二つ走らせる方法である。
- いずれの方法を取るにせよ、ノード間の並列化はMPIを使う。 ノード間、ノード内、どちらもMPIで並列化する前者の方法をflat MPI並列化と呼ぶ。
- ノード間はMPIで、ノード内はOpenMPで並列化する後者の方法はhybrid並列化と呼ぶ。
【演習】flat MPI並列化 †
- まずはflat MPIを試してみよう。
- 128個のMPIプロセスを64ノードで走らせる。 方法は簡単。ジョブスクリプトを少し変えるだけで良い。
- 参考ジョブスクリプト( flatmpi.128.js )
#!/bin/sh
#PBS -l cputim_job=00:05:00
#PBS -l memsz_job=2gb
#PBS -l cpunum_job=2
#PBS -T vltmpi
#PBS -b 64
#PBS -q PCL-A
cd /home/users/yourdirectory
mpirun_rsh -np 128 ${NQSII_MPIOPTS} ./a.out
- 実行結果例。 64ノード(128MPIプロセス)で計算した結果を下に示す。 デュアルコアのうち一つのコアを遊ばせていた上記の場合(計算時間3.2秒)に比べると、ディアルコアを全部使いきったこの時、計算時間は半分とまでいかないが、2.4秒まで短縮された。
[0] stopwatch: 0 2.393928 # 全実行時間 (約2.4秒) [0] stopwatch: 1 0.7410951 # 並列初期化にかかった時間 [0] stopwatch: 2 2.4318695E-04 # 温度場初期化にかかった時間 [0] stopwatch: 3 1.652695 # temperature__updateにかかった時間 [0] stopwatch: 4 0.5054324 # MPI通信にかかった時間 [0] stopwatch: 5 1.3842821E-02 # 境界条件の設定にかかった時間 [0] stopwatch: 6 0.6929536 # ヤコビ法のメインループにかかった時間 [0] stopwatch: 7 0.4263895 # 作業配列を温度場にコピーするのにかかった時間 [0] stopwatch: 8 1.650211 # temperature__updateにかかった時間
- ここまで並列化を進めると、ヤコビ法のメインループにかかった時間(上の6番、約0.7秒)と比較して、 MPI通信にかかる時間(下の4番、0.5秒)の割合はかなり大きくなってくる。
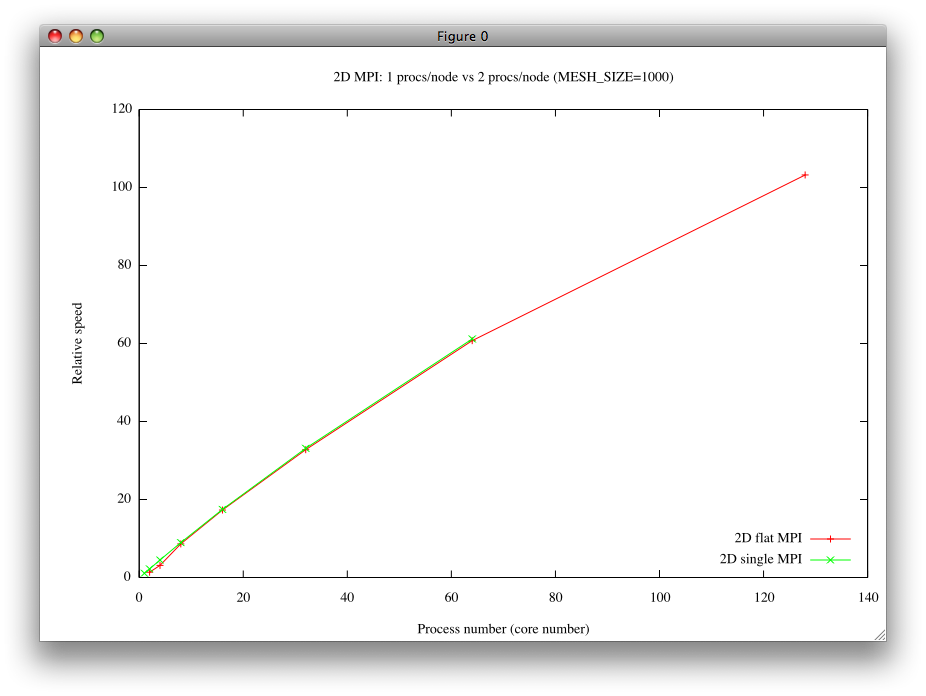
- flat MPI並列化を行った場合とデュアルコアの半分を遊ばせた場合との速度の比較を下のグラフに示した。
hybrid並列化 †
- 次にhybrid並列化を試してみよう。
- 方法は簡単。一つのノードに一つのMPIプロセスを走らせ、計算時間の最もかかるdo-loop部分―いまの場合はヤコビ法の部分―だけを「4. OpenMPを使った並列計算」で学んだ方法で二つのスレッドにforkさせて計算すればよい。 このときデュアルコアが二つとも仕事をしている。
hybrid並列化法による熱伝導コード †
- ファイル名:thermal_diffusion_decomp2d_hybrid.f90
- OpenMPによるスレッド並列化のためにコードに加える変更はわずかである。実際、
diff thermal_diffusion_decomp2d_mpi.f90 thermal_diffusion_decomp2d_hybrid.f90
をとってみると、その結果は以下の通りである(本質的でない差分は削除した):
380a380 > use omp_lib 496a497 > !$omp parallel do 502a504 > !$omp end parallel do 505c507,514 < temp(istt:iend,jstt:jend) = work(istt:iend,jstt:jend) --- > ! temp(istt:iend,jstt:jend) = work(istt:iend,jstt:jend) > !$omp parallel do > do j = jstt , jend > do i = istt , iend > temp(i,j) = work(i,j) > end do > end do > !$omp end parallel do 513c522
- hybrid並列化ジョブ投入用ジョブスクリプト(hybrid.js) これは64ノードを使い、1ノードあたり1MPIプロセス、二つのOpenMPスレッドを走らせる時のスクリプトである。
#!/bin/sh
#PBS -l cputim_job=00:05:00
#PBS -l memsz_job=2gb
#PBS -l cpunum_job=1
#PBS -T vltmpi
#PBS -v OMP_NUM_THREADS=2
#PBS -b 64
#PBS -q PCL-A
cd /home/users/yourname
mpirun_rsh -np 64 ${NQSII_MPIOPTS} ./a.out
【演習】hybrid並列化 †
- 上のジョブスクリプトを使い、64ノードを使ったhybrid並列化による計算を行え。
- hybrid並列化を行うときのコンパイルコマンドは以下の通りである。
mpif90 -mp thermal_diffusion_decomp2d_hybrid.f90
- 実行結果例
[0] stopwatch: 0 2.007206 # 全実行時間 (約2.0秒) [0] stopwatch: 1 0.3776278 # 並列初期化にかかった時間 [0] stopwatch: 2 3.4689903E-04 # 温度場初期化にかかった時間 [0] stopwatch: 3 1.629401 # temperature__updateにかかった時間 [0] stopwatch: 4 0.4579115 # MPI通信にかかった時間 [0] stopwatch: 5 1.6872644E-02 # 境界条件の設定にかかった時間 [0] stopwatch: 6 0.7087350 # ヤコビ法のメインループにかかった時間 [0] stopwatch: 7 0.4316428 # 作業配列を温度場にコピーするのにかかった時間 [0] stopwatch: 8 1.626958 # temperature__updateにかかった時間
- flat MPIで計算した場合(約2.4)よりも20%近く高速化されている。 並列化を全く行わない場合 (約157秒)に比べると約78倍の高速化である。
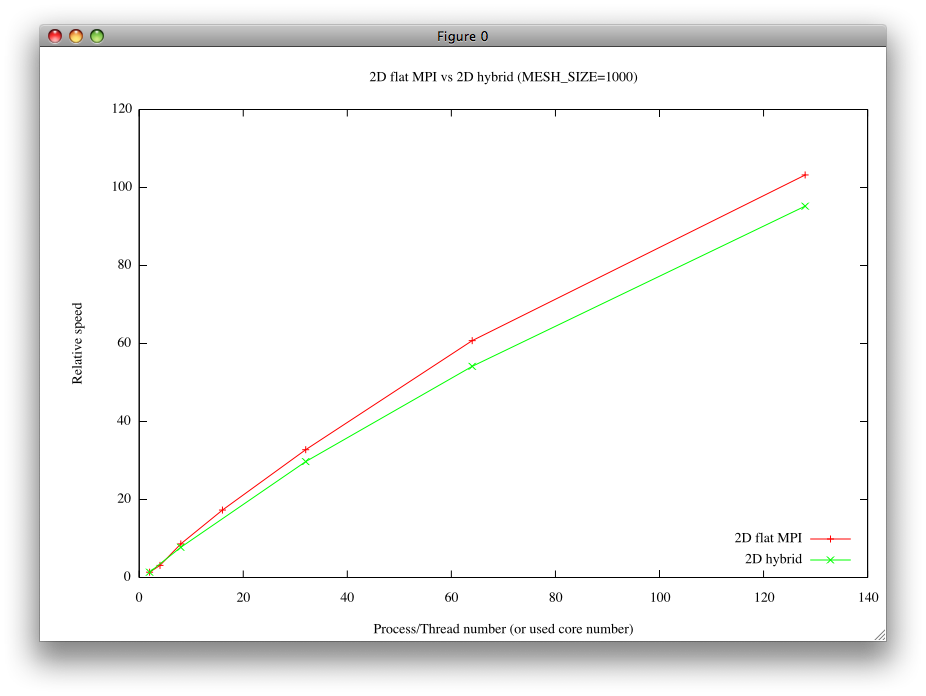
- 実は、コンパイルオプションを変えると、さらに高速化される。 (詳しくは述べない。) このとき、flat MPI並列化の方がhybrid並列化よりも速くなる。 両者の計算速度を比較した図を下に示す。
レポート課題 †
- 次の2種類のグラフを描き、それぞれのグラフが意味すること考察せよ。
- 【グラフ1】
- 熱伝導問題をhybrid並列化によって解くコード(thermal_diffusion_decomp2d_hybrid.f90)を使い、 使用するコア数と計算速度の関係を示すグラフを描け。 (つまり上の図の緑色のグラフと同じものを自分で計測して描けということ。)
- 横軸は使用するコア数とする。範囲は2から128まで。サンプル点数は任意。
- 縦軸を「計算速度」とし、それはプログラムの全実行時間の逆数とする。
- 注意1: 上の緑色のグラフは特別なコンパイルオプションで計算したので、グラフ形状は違うはず。縦軸のスケールも違う。
- 注意2:グラフを描くのに、必ずしもgnuplotを使う必要はない。他のグラフソフトを使用しても可。
- 補足: 参考までに上に示したグラフを描くときに使ったgnuplotスクリプトを /tmp/100722/plot03.gp においた。
- 【グラフ2】
- 横軸は同じ(使用コア数)とし、縦軸に「プログラムの全実行時間の中でMPI通信にかかった時間の割合」を示すグラフを描け。
- ヒントは0番と4番のstopwatch出力。
レポート提出方法 †
- 提出先: 自然科学棟4号館 8階 陰山研究室(エレベータ降りてすぐ前の部屋)
- 提出期限: 2010年7月29日17時
- 注意: レポートには氏名と共に学籍番号も記入すること。
アンケート †
- 難易度について: この「計算科学演習 I 」全体を通じてどうでしたか?(どれか一つ、一度だけ押してください。)
- 演習の量について: この「計算科学演習 I 」全体を通じ、講義の時間に対して、演習にかける時間の割合はどうでしたか?(どれか一つ、一度だけ押してください。)
- 並列計算についての印象: 並列計算についてどう感じましたか?(どれか一つ、一度だけ押してください。)
- 計算科学について: この演習を通じて、並列計算機を駆使した科学技術計算や計算科学について、興味が高まり、自分でもやってみたいという意欲を感じましたか?(どれか一つ、一度だけ押してください。)
- 質問・コメント自由記入
- 今回の計算科学演習全体に関して質問、コメントなど自由に書き込んでください。
- 「お名前」欄は空欄で可。
コメントはありません。 コメント/7.実践編?
as of 2025-08-23 (土) 04:24:55 (7734)