PukiWiki - 6.1 MPI並列計算の復習のバックアップ(No.1)

バックアップ一覧
差分を表示
現在との差分を表示
ソースを表示
6.1 MPI並列計算の復習へ行く。
- 1 (2010-07-08 (木) 11:31:58)
- 2 (2010-07-08 (木) 12:13:00)

神戸大学大学院システム情報学研究科計算科学専攻陰山聡

この演習で示すソースコードは /tmp/100708 に置いた。

【2010.07.08: 講義後追記】変更箇所

スクリプトでgnuplotを使う場合、グラフがグラフが一瞬描かれた直後に終了してしまうという問題があった。これを避けるにはgnuplotスクリプトの最後の一行に
```
pause -1
```
と書く必要がある。以下のコンテンツではこの点に修正を加えた。
ソースコードheat1_animation_x_prof.f90が抜けていた問題を修正した。

【目次】

前回のレポート（並列化）の解説
MPI通信の確認
- ジョブスクリプト
【演習】
- 結果例

前回のレポート（並列化）の解説 †

↑

問題設定の復習 †

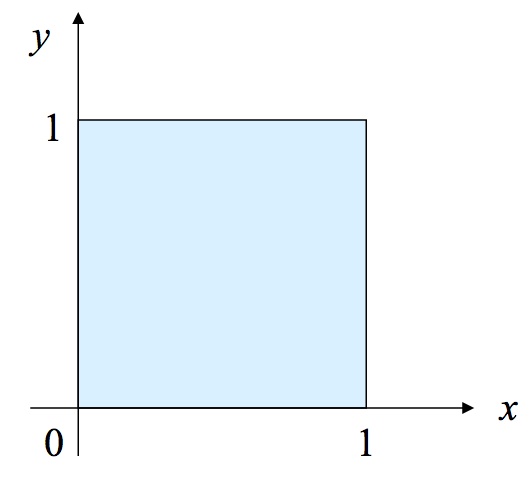
2次元正方形領域 [0,1]×[0,1] での熱伝導を考える
境界をすべて0℃に固定
領域全体に一定の熱を加える
⇒ このとき，十分な時間が経った後での温度分布はどうなるか？

↑

非並列版コードの復習 †

熱伝導とは注目する一点が、「近所」の温度と等しくなろうという傾向である。 ⇒周囲の温度の平均値になろうとする。熱源があれば、一定の割合で温度が上がろうとする。

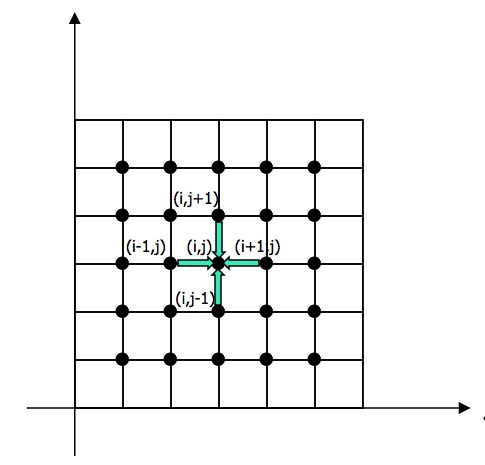
ヤコビ法アルゴリズム。

do j=1, m
    do i=1, m
        u_new(i,j) = ( u(i-1,j) + u(i+1,j) + u(i,j-1) + u(i,j+1) ) / 4 + f(i,j)
    end do
end do

このヤコビ法に基づいたコード heat1.f90を前回の演習で学んだ。

↑

heat1_wi_comments.f90 （詳細コメント付きバージョン） †

後の改訂に備えて、まずこのheat1.f90を少し丁寧に復習しよう。

! 
! heat1_wi_comments.f90
!
!-----------------------------------------------------------------------
! Time development form of the thermal diffusion equation is
!    \partial T(x,y,t) / \partial t = \nabla^2 T(x,y,t) + heat_source.
! In the stationary state, 
!    \nabla^2 T(x,y) + heat_source = 0.
! The finite difference method with grid spacings dx and dy leads to
!    (T(i+1,j)-2*T(i,j)+T(i-1,j))/dx^2 
!  + (T(i,j+1)-2*T(i,j)+T(i,j-1))/dy^2 + heat_source = 0.
! When dx=dy=h,
!    T(i,j) = (T(i+1,j)+T(i-1,j)+T(i,j+1)+T(i,j-1))/4+heat_source*h^2/4.
! This suggests a relaxation method called Jacobi method adopted in
! this code.
!-----------------------------------------------------------------------

program heat1_wi_comments
  implicit none
  integer, parameter :: m=31            ! mesh size
  integer            :: nmax=20000      ! max loop counter
  integer :: i,j,n
  integer, parameter :: SP = kind(1.0)
  integer, parameter :: DP = selected_real_kind(2*precision(1.0_SP))
  real(DP), dimension(:,:), allocatable :: u    ! temperature field
  real(DP), dimension(:,:), allocatable :: un   ! work array
  real(DP) :: heat=1.0_DP       ! heat source term; uniform distribution.
  real(DP) :: h                 ! grid size

  !                    |<----- 1.0 ----->|
  !               j=m+1+-------u=0-------+  ---
  !               j=m  |                 |   ^
  !                .   |                 |   | 
  !                .   |     uiform      |   | 
  !                   u=0    heat       u=0 1.0   
  ! j-direction    .   |     source      |   | 
  !(y-direction)  j=2  |                 |   | 
  !     ^         j=1  |                 |   v 
  !     |         j=0  +-------u=0-------+  ---
  !     |             i=0 1 2 ...      i=m+1
  !     |
  !     +-------> i-direction (x-direction)
  !
  ! when m = 7, 
  !       |<-------------------- 1.0 -------------------->|
  !       |                                               |
  !       |  h     h     h     h     h     h     h     h  |
  !       |<--->|<--->|<--->|<--->|<--->|<--->|<--->|<--->|
  !       +-----+-----+-----+-----+-----+-----+-----+-----+
  !     i=0     1     2     3     4     5     6     7     8 
  !
  allocate( u(0:m+1,0:m+1) )    ! memory allocation of 2-D array.
                                ! you can access each element of u
                                ! as u(i,j), where 0<=i<=m+1 
                                ! and  0<=j<=m+1.

  allocate( un(m,m) )           ! another memory allocation. in
                                ! this case un(i,j) with
                                ! 1<=i<=m and 1<=j<=m.

  h = 1.0_DP/(m+1)              ! grid spacing.

  u(:,:) = 0.0_DP  ! initial temperature is zero all over the square.

  do n = 1 , nmax     ! relaxation loop 
    do j = 1 , m      ! in the y-direction
      do i = 1 , m
        un(i,j)=(u(i-1,j)+u(i+1,j)+u(i,j-1)+u(i,j+1))/4.0_DP+heat*h*h
      end do
    end do                      ! same as the following do-loops:
    u(1:m,1:m) = un(1:m,1:m)    ! do j = 1 , m
                                !   do i = 1 , m
                                !     u(i,j) = un(i,j)
                                !   end do
                                ! end do
    if ( mod(n,100)==0 ) print *, n, u(m/2+1,m/2+1)  ! temperature at
  end do                                             ! the center
end program heat1_wi_comments

↑

再びheat1.f90（コメントなしバージョン） †

次に詳しいコメントをはずしてもう一度もとのheat1.f90を見てみる。（ただし、先週のコードから本質的でないところを少しだけ修正している。）

program heat1
  implicit none
  integer, parameter :: m=31, nmax=20000
  integer :: i,j,n
  integer, parameter :: SP = kind(1.0)
  integer, parameter :: DP = selected_real_kind(2*precision(1.0_SP))
  real(DP), dimension(:,:), allocatable :: u, un
  real(DP) :: h, heat=1.0_DP

  allocate(u(0:m+1,0:m+1))
  allocate(un(m,m))

  h=1.0_DP/(m+1)
  u(:,:) = 0.0_DP

  do n=1, nmax
    do j=1, m
      do i=1, m
        un(i,j)=(u(i-1,j)+u(i+1,j)+u(i,j-1)+u(i,j+1))/4.0_DP+heat*h*h
      end do
    end do
    u(1:m,1:m)=un(1:m,1:m)
    if (mod(n,100)==0) print *, n, u(m/2+1,m/2+1)
  end do
end program heat1

↑

先週の課題（演習3-3） †

heat1.f90 を MPI を用いて並列化せよ

↑

解答例（heat2.f90） †

program heat2
  use mpi
  implicit none
  integer, parameter :: m=31, nmax=20000
  integer :: i,j,jstart,jend,n
  integer, parameter :: SP = kind(1.0)
  integer, parameter :: DP = selected_real_kind(2*precision(1.0_SP))
  real(DP), dimension(:,:), allocatable :: u, un
  real(DP) :: h, heat=1.0_DP
  integer ::  nprocs,myrank,ierr,left,right
  integer, dimension(MPI_STATUS_SIZE) :: istat

  call mpi_init(ierr)
  call mpi_comm_size(MPI_COMM_WORLD,nprocs,ierr)
  call mpi_comm_rank(MPI_COMM_WORLD,myrank,ierr)

  h = 1.0_DP/(m+1)

  jstart = m*myrank/nprocs+1
  jend   = m*(myrank+1)/nprocs

  allocate( u(0:m+1,jstart-1:jend+1))
  allocate(un(    m,  jstart:jend  ))

  u(:,:) = 0.0_DP

  left = myrank-1
  if ( myrank==0 )        left  = nprocs-1
  right = myrank+1
  if ( myrank==nprocs-1 ) right = 0

  do n=1, nmax
    call mpi_sendrecv(u(1,jend),m,MPI_DOUBLE_PRECISION,right,100,       &
                      u(1,jstart-1),m,MPI_DOUBLE_PRECISION,left,100,    &
                      MPI_COMM_WORLD,istat,ierr)
    call mpi_sendrecv(u(1,jstart),m,MPI_DOUBLE_PRECISION,left,100,      &
                      u(1,jend+1),m,MPI_DOUBLE_PRECISION,right,100,     &
                      MPI_COMM_WORLD,istat,ierr)

    if (myrank==0)        u(1:m,  0) = 0.0_DP
    if (myrank==nprocs-1) u(1:m,m+1) = 0.0_DP

    do j = jstart , jend
      do i = 1 , m
        un(i,j)=(u(i-1,j)+u(i+1,j)+u(i,j-1)+u(i,j+1))/4.0_DP+heat*h*h
      end do
    end do
    u(1:m,jstart:jend)=un(1:m,jstart:jend)

    if (jstart<=m/2+1 .and. jend>=m/2+1) then
      if (mod(n,100)==0) print *, n, u(m/2+1,m/2+1)
    end if
  end do
  call mpi_finalize(ierr)
end program heat2

↑

コード解説（コメント付きソースコード heat2_wi_comments.f90） †

上のheat2.f90を解説するために詳しいコメントをつけたソースコードheat2_wi_comments.f90を以下に示す。

program heat2_wi_comments
  use mpi
  implicit none
  integer, parameter :: m=31            ! mesh size
  integer, parameter :: nmax=20000      ! max loop counter
  integer :: i,j,jstart,jend,n
  integer, parameter :: SP = kind(1.0)
  integer, parameter :: DP = selected_real_kind(2*precision(1.0_SP))
  real(DP), dimension(:,:), allocatable :: u  ! temperature field
  real(DP), dimension(:,:), allocatable :: un ! work array
  real(DP) :: heat=1.0_DP   ! heat source term. uniform distribution.
  real(DP) :: h             ! grid spacing; dx=dy=h
  integer  :: nprocs        ! number of MPI processes
  integer  :: myrank        ! my rank number
  integer  :: left, right   ! nearest neighbor processes
  integer, dimension(MPI_STATUS_SIZE) :: istat ! used for MPI
  integer  :: ierr          ! used for mpi routines

  call mpi_init(ierr)
  call mpi_comm_size(MPI_COMM_WORLD,nprocs,ierr)
  call mpi_comm_rank(MPI_COMM_WORLD,myrank,ierr)

  h = 1.0_DP/(m+1)          ! grid spacings. see the comment fig below.

  jstart = m*myrank/nprocs+1   ! the process is in charge of this point
  jend   = m*(myrank+1)/nprocs ! point to this point. see the fig below.

!- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
!
! when m = 7, nprocs = 3
! 
!     |<-------------------- 1.0 -------------------->|      
!     |                                               |
!     |  h  |  h     h     h     h     h     h     h  |
!     |<--->|<--->|<--->|<--->|<--->|<--->|<--->|<--->|
!     |     |     |     |     |     |     |     |     |
!     +-----+-----+-----+-----+-----+-----+-----+-----+
!   j=0     1     2     3     4     5     6     7     8
!     +-----+-----+-----+-----+-----+-----+-----+-----+
!     |  jstart   |     |           |     |     |     | 
!     |     |   jend    |           |   jstart  |     | 
!     o-----rank=0------o           |     |    jend   |
!                 |     |           |     |     |     |
!                 |   jstart      jend    |     |     |
!                 |     |           |     |     |     |
!                 o------- rank=1---------o     |     |
!                                   |     |     |     | 
!                                   o------rank=2-----o
!
!- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
!
! Another example, when m=17, nprocs=6
!
!  j=0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18
!    +--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+
!    |        |        |     |           |        |        |
!    o==rank0=o        |     o===rank3===o        |        |
!          |           |        |     |           |        |
!          o===rank1===o        |     o===rank4===o        |
!                   |           |              |           |
!                   o===rank2===o              o===rank5===o
! each process      |           |
! has 2D array  u[i,jstart-1:jend+1] 
!
!- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

  allocate( u(0:m+1,jstart-1:jend+1)) ! 2-D array for temperature.
  allocate(un(m,jstart:jend))         ! 2-D work array.
  u(:,:) = 0.0_DP

  left  = myrank-1  ! left neighbor.
  if (myrank==0)        left = nprocs-1  ! a dummy periodic distribution
  right = myrank+1  ! right neighbor.    ! for code simplicity. this has
  if (myrank==nprocs-1) right = 0        ! actually no effect.

  do n = 1 , nmax   ! main loop for the relaxation, to equilibrium.
    !- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
    !
    !                  jend                          jstart      
    !   <(left)>        |                              |    <(right)>
    !      - --o--o--o--o--o                        o--o--o--o--o-- -
    !              send |  ^ recv                   ^  |
    !                   |  |                        |  |
    !                 [2]  [3]                    [1]  [4]
    !                   |  |                        |  |
    !              recv v  | send                   |  v
    !                   o--o--o--o-- - - --o--o--o--o--o
    !                      |                        |
    !                    jstart                    jend
    !                               <(myself)>
    !                     
    !- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
    call mpi_sendrecv(u(1,jend),    m,MPI_DOUBLE_PRECISION,right,100,  & ! [1]
                      u(1,jstart-1),m,MPI_DOUBLE_PRECISION,left,100,   & ! [2]
                      MPI_COMM_WORLD,istat,ierr)
    call mpi_sendrecv(u(1,jstart),m,MPI_DOUBLE_PRECISION,left, 100,    & ! [3]
                      u(1,jend+1),m,MPI_DOUBLE_PRECISION,right,100,    & ! [4]
                      MPI_COMM_WORLD,istat,ierr)

    if (myrank==0)        u(1:m,0  ) = 0.0_DP   ! to keep the boundary 
    if (myrank==nprocs-1) u(1:m,m+1) = 0.0_DP   ! condition (temp=0).

    do j = jstart , jend   ! Jacobi method. 
      do i = 1 , m         ! no need to calculate the boundary i=0 and m+1.
        un(i,j)=(u(i-1,j)+u(i+1,j)+u(i,j-1)+u(i,j+1))/4.0_DP+heat*h*h
      end do
    end do
    u(1:m,jstart:jend)=un(1:m,jstart:jend) ! this is actually doubled do-loops.

    if (jstart<=m/2+1 .and. jend>=m/2+1) then         ! print out the temperature
      if (mod(n,100)==0) print *, n, u(m/2+1,m/2+1)   ! at the central grid point.
    end if
  end do

  deallocate(un,u)        ! or you can call deallocate for two times for un and u.
  call mpi_finalize(ierr)    
end program heat2_wi_comments

↑

MPI通信の確認 †

前回の演習で説明されたMPI_SENDRECVの挙動を改めて確認しよう。そのためのソースコード（heat2_sendrecv_check.f90）を以下に用意した。これは上記のheat2.f90からヤコビ法による熱伝導問題の解法部分を除き、 MPIの通信に関係する部分だけを抜き出したものである。

!- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
!
! when m = 7, nprocs = 3
! 
!     |<-------------------- 1.0 -------------------->|      
!     |                                               |
!     |  h  |  h     h     h     h     h     h     h  |
!     |<--->|<--->|<--->|<--->|<--->|<--->|<--->|<--->|
!     |     |     |     |     |     |     |     |     |
!     +-----+-----+-----+-----+-----+-----+-----+-----+
!   j=0     1     2     3     4     5     6     7     8
!     +-----+-----+-----+-----+-----+-----+-----+-----+
!     |  jstart   |     |           |     |     |     | 
!     |     |   jend    |           |   jstart  |     | 
!     o==== rank=0 =====o           |     |    jend   |
!                 |     |           |     |     |     |
!                 |   jstart      jend    |     |     |
!                 |     |           |     |     |     |
!                 o======= rank=1 ========o     |     |
!                                   |     |     |     | 
!                                   o===== rank=2 ====o
!
!- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
!
! Another example, when m=17, nprocs=6
!
!  j=0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18
!    +--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+
!    |        |        |     |           |        |        |
!    o==rank0=o        |     o===rank3===o        |        |
!          |           |        |     |           |        |
!          o===rank1===o        |     o===rank4===o        |
!                   |           |              |           |
!                   o===rank2===o              o===rank5===o
! each process      |           |
! has 2D array  u[i,jstart-1:jend+1] 
!
!- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
!  
program heat2_sendrecv_check
  use mpi
  implicit none
  integer, parameter :: m=17
  integer :: i,j,jstart,jend,n
  integer, parameter :: SP = kind(1.0)
  integer, parameter :: DP = selected_real_kind(2*precision(1.0_SP))
  real(DP), dimension(:,:), allocatable :: u, un
  integer ::  nprocs,myrank,ierr,left,right
  integer, dimension(MPI_STATUS_SIZE) :: istat

  call mpi_init(ierr)
  call mpi_comm_size(MPI_COMM_WORLD,nprocs,ierr)
  call mpi_comm_rank(MPI_COMM_WORLD,myrank,ierr)

  jstart = m*myrank/nprocs+1
  jend   = m*(myrank+1)/nprocs

  allocate( u(0:m+1,jstart-1:jend+1))
  allocate(un(    m,  jstart:jend  ))

  u(:,jstart-1:jend+1) = myrank

  call print('before',myrank, jstart, jend, u(m/2+1,:))

  left = myrank-1
  if ( myrank==0 )        left  = nprocs-1
  right = myrank+1
  if ( myrank==nprocs-1 ) right = 0

  !- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  !
  !                  jend                          jstart      
  !   <(left)>        |                              |    <(right)>
  !      - --o--o--o--o--o                        o--o--o--o--o-- -
  !              send |  ^ recv                   ^  |
  !                   |  |                        |  |
  !                 [2]  [3]                    [1]  [4]
  !                   |  |                        |  |        
  !                   |  |                        |  |
  !              recv v  | send                   |  v
  !                   o--o--o--o-- - - --o--o--o--o--o
  !                      |                        |
  !                    jstart                    jend
  !                               <(myself)>
  !                     
  !- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

  call mpi_sendrecv(u(1,jend),    m,MPI_DOUBLE_PRECISION,right,100,   & ! [1]
                    u(1,jstart-1),m,MPI_DOUBLE_PRECISION, left,100,   & ! [2]
                    MPI_COMM_WORLD,istat,ierr)
  call mpi_sendrecv(u(1,jstart),m,MPI_DOUBLE_PRECISION, left,100,     & ! [3]
                    u(1,jend+1),m,MPI_DOUBLE_PRECISION,right,100,     & ! [4]
                    MPI_COMM_WORLD,istat,ierr)

!   if (myrank==0)        u(1:m,  0) = 0.0_DP
!   if (myrank==nprocs-1) u(1:m,m+1) = 0.0_DP

  call print(' after', myrank, jstart, jend, u(m/2+1,:))

  deallocate(u,un)
  call mpi_finalize(ierr)

contains

  subroutine print(message,myrank,jstart,jend,u)
    character(len=*), intent(in)                     :: message
    integer,          intent(in)                     :: myrank
    integer,          intent(in)                     :: jstart
    integer,          intent(in)                     :: jend
    real(DP), dimension(jstart-1:jend+1), intent(in) :: u

    integer, dimension(0:m+1) :: iu          ! work array of integer
    integer                   :: rank, ierr
    character(len=100)        :: line        ! printed line on stdout
    character(len=20)         :: format      ! print format
    
    iu(:) = -1    ! initialization of the work integer array.
    iu(jstart-1:jend+1) = u(jstart-1:jend+1) ! copy the data (double to int).

    write(format,'(i3"(i3)")') m+2     ! format	string generator. 
    write(line,format) (iu(i),i=0,m+1) ! integers to a text line.

    do rank = 0 , nprocs-1                   ! to avoid random printing
       call mpi_barrier(MPI_COMM_WORLD,ierr) ! by each process in random order,
       if ( rank==myrank ) then              ! we here put the loop and barrier.
          print *, message//':'//trim(line)
       end if
    end do
  end subroutine print

end program heat2_sendrecv_check

↑

ジョブスクリプト †

このコード（heat2_sendrecv_check.f90）をscalarに投入するためのジョブスクリプトを以下のように設定すると、heat2_sendrecv_check.f90のコメントに書いた例と同じ、プロセス数が6のジョブを投入できる。

#PBS -l cputim_job=00:05:00
#PBS -l memsz_job=2gb
#PBS -l cpunum_job=1
#PBS -T vltmpi
#PBS -b 6
#PBS -q PCL-A

cd /home/users/yourID/YourDirectory
mpirun_rsh -np 6 ${NQSII_MPIOPTS} ./a.out

↑

【演習】 †

heat2_sendrecv_check.f90をmpif90コマンドでコンパイルし、上記ジョブスクリプトを heat2_sendrecv_check.jsという名前のファイルに保存した上で、

qsub heat2_sendrecv_check.js

としてジョブを投入せよ。

(2) MPIプロセス数やグリッドサイズmを変えて試せ。

↑

結果例 †

%NQSII(INFO): ------- Output from job:0000 -------
[0]  before:  0  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
[0]   after:  5  0  0  1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
%NQSII(INFO): ------- Output from job:0001 -------
[1]  before: -1 -1  1  1  1  1  1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
[1]   after: -1 -1  0  1  1  1  2 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
%NQSII(INFO): ------- Output from job:0002 -------
[2]  before: -1 -1 -1 -1 -1  2  2  2  2  2 -1 -1 -1 -1 -1 -1 -1 -1 -1
[2]   after: -1 -1 -1 -1 -1  1  2  2  2  3 -1 -1 -1 -1 -1 -1 -1 -1 -1
%NQSII(INFO): ------- Output from job:0003 -------
[3]  before: -1 -1 -1 -1 -1 -1 -1 -1  3  3  3  3  3 -1 -1 -1 -1 -1 -1
[3]   after: -1 -1 -1 -1 -1 -1 -1 -1  2  3  3  3  4 -1 -1 -1 -1 -1 -1
%NQSII(INFO): ------- Output from job:0004 -------
[4]  before: -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1  4  4  4  4  4 -1 -1 -1
[4]   after: -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1  3  4  4  4  5 -1 -1 -1
%NQSII(INFO): ------- Output from job:0005 -------
[5]  before: -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1  5  5  5  5  5
[5]   after: -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1  4  5  5  5  0

as of 2023-09-22 (金) 23:13:09 (4753)

6.1 MPI並列計算の復習のバックアップ(No.1)

前回のレポート（並列化）の解説 †

問題設定の復習 †

非並列版コードの復習 †

heat1_wi_comments.f90 （詳細コメント付きバージョン） †

再びheat1.f90（コメントなしバージョン） †

先週の課題（演習3-3） †

解答例（heat2.f90） †

コード解説（コメント付きソースコード heat2_wi_comments.f90） †

MPI通信の確認 †

ジョブスクリプト †

【演習】 †

結果例 †

演習について

計算科学演習A1

計算科学演習A2

πコンピュータ利用ガイド

このサイトについて

お問い合わせ

サイト内検索

6.1 MPI並列計算の復習 のバックアップ(No.1)

前回のレポート（並列化）の解説 †

問題設定の復習 †

非並列版コードの復習 †

heat1_wi_comments.f90 （詳細コメント付きバージョン） †

再びheat1.f90（コメントなしバージョン） †

先週の課題（演習3-3） †

解答例（heat2.f90） †

コード解説 （コメント付きソースコード heat2_wi_comments.f90） †

MPI通信の確認 †

ジョブスクリプト †

【演習】 †

結果例 †

演習について

計算科学演習A1

計算科学演習A2

πコンピュータ利用ガイド

このサイトについて

お問い合わせ

サイト内検索

6.1 MPI並列計算の復習のバックアップ(No.1)

コード解説（コメント付きソースコード heat2_wi_comments.f90） †