- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 7.1 MPIによる2次元並列化 へ行く。
- 1 (2010-07-14 (水) 17:42:56)
- 2 (2010-07-14 (水) 19:39:36)
- 3 (2010-12-28 (火) 16:05:30)
- 4 (2012-01-10 (火) 17:48:51)
- 5 (2018-08-01 (水) 13:21:42)
- 6 (2018-10-16 (火) 17:13:48)
- 7 (2019-06-11 (火) 17:44:59)
- 8 (2019-07-31 (水) 14:46:05)
- 9 (2020-06-25 (木) 07:56:25)
- 10 (2021-05-29 (土) 03:51:30)
- 11 (2021-08-05 (木) 18:29:51)
- 12 (2021-08-08 (日) 12:32:08)
- 13 (2023-05-06 (土) 10:29:21)
- 14 (2024-01-02 (火) 22:14:41)
現在(2024-04-17 (水) 17:01:04)作成中です。 既に書いている内容も大幅に変わる可能性が高いので注意。
神戸大学 大学院システム情報学研究科 計算科学専攻 陰山 聡
【目次】
2次元並列化 †
- 引き続き、正方形領域の熱伝導問題(平衡温度分布)を解く例題を扱う。
- これまでMPIで並列化を行うにあたり、正方形領域のy方向(j方向)に複数の領域に分割し、 それぞれの領域に一つずつMPIプロセスを割り当てて並列化していた。 このような並列化を1次元領域分割による並列化という。 下の図は正方形領域を16個の領域に分割した例である。
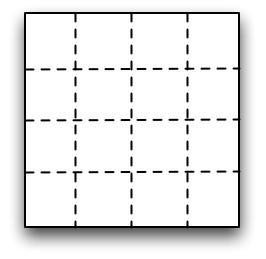
- 同様に二次元領域分割による並列化も考えられる。 正方形を16個の領域に2次元的に分割すると下の図のようになる。
- 上の二つの図はどちらも16個のMPIプロセスで並列化しているので、 計算速度の点で見ればどちらも同じと思うかもしれない。
- だがそれは違う。 プロセス間の通信にかかる時間がゼロであれば、そのとおりだが、実際にはプロセス間の通信(MPI_SENDやMPI_RECV等)には有限の―それどころかかなり長い―時間がかかる。
- では、プロセス間通信に長い時間がかかるという前提の下で、 1次元領域分割と、2次元領域分割ではどちらが計算が速いであろうか?
- 下の図は正方形領域を400個の格子点で離散化した場合を示す。
- これを4つのMPIプロセスで並列化することを考える。 1次元領域分割の場合、下の図のようになる。
- 2次元領域分割の場合、同じく4つのMPIプロセスで並列化すると、下の図のようになる。
授業アンケート †
今回の演習内容はどうでしたか?(どれか一つ、一度だけ押してください。)
質問、コメントなど自由にどうぞ †
「お名前」欄は空欄で可。
コメントはありません。 コメント/7.1 MPIによる2次元並列化?
as of 2025-08-23 (土) 04:26:39 (3421)